De legende van de Torens van Hanoi. De Torens van Hanoi is een spel of puzzel met een aantal schijven. Het spel bestaat uit een plankje met daarop drie stokjes. Aan het begin van het spel is op een van de stokjes een kegelvormige toren geplaatst van schijven met een gat in het midden. De schijven hebben verschillende diameters, in toenemende grootte. Ze zijn zo geplaatst dat de kleinste schijf bovenop en de grootste onderop ligt. 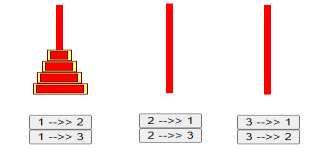Het doel van het spel is om de complete toren van schijven te verplaatsen naar een ander stokje, waarbij de volgende regels in acht genomen dienen te worden: - Er mag slechts 1 schijf tegelijk worden verplaatst. - Nooit mag een grotere schijf op een kleinere rusten. Om praktische redenen heeft de toren meestal 8 schijfjes, omdat een spel met dit aantal binnen een minuut of 6 op te lossen is.

Het spel is uitgevonden door de Franse wiskundige Edouard Lucas in 1883. Er is een legende over een hindoe-tempel in de Indiase stad Benares onder keizer Fo Hi, waarvan de priesters, de Brahmanen, zich bezighouden met het verplaatsen van een toren van 64 gouden schijven. De schijven liggen op drie naalden van diamant, een el lang en zo dik als het lichaam van een bij. Volgens de legende komt de wereld tot een einde als het werk af is. Het is niet duidelijk of Lucas deze legende bedacht heeft of er alleen door is geïnspireerd. Stel dat de priesters 1 schijf per seconde verplaatsen, dan zullen we straks zien hoe lang we nog met deze wereld te gaan hebben. Eerst maar een een eenvoudig geval bekijken: n = 3 schijven Hoeveel handelingen heeft dit gekost? En nu n = 4 schijven. Hoeveel handelingen heeft dit gekost? Speel HIER het spel zelf, eerst met 3, dan 4 en dan 5 schijven. Ik ben geïnteresseerd in het aantal handelingen zoiets je (minimaal) moet verrichten!

Met recursie kunnen we een rij maken van het aantal benodigde handelingen voor n = 1 , 2 , 3 , 4, ......... Het werkt als volgt: - Stel dat we een oplossing hebben om een toren van n schijven te verplaatsen, en dat dat An zetten kost. - Dan weet ik hoe je een toren van n + 1 schijven kunt verplaatsen. Dat gaat in drie stappen:       stap 1: Verplaats de bovenste n schijven naar een andere stok. Dat kost An zetten       stap 2: Verplaats de onderste schijf naar de nu lege stok. Dat kost 1 zet       stap 3: Verplaats de toren van n schijven boven op de grootste schijf. Dat kost weer An zetten. In totaal kost een toren van n + 1 schijven dan An+1 = An + 1 + An = 2×An + 1 zetten En we weten hoeveel een toren van één schijf kost; namelijk 1 zet, Dus A1 = 1.

Gebruik nu deze recursieve formule, en zet de GRM aan het werk om te berekenen hoeveel seconden onze wereld nog heeft te gaan volgens deze legende. Omzetten in jaren: 60 × 60 × 24 × 365,24 = 31556736 seconden. Leeftijd van het heelal sinds de "Big Bang" is ongeveer 13,7 miljard jaar, met een foutmarge van 1%.