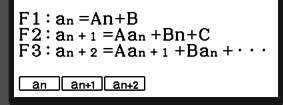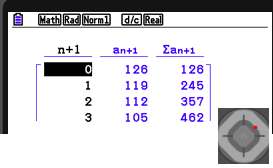
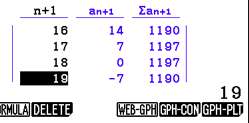
Sint Maarten (een simpel voorbeeld om de werking van de GRM te leren) Een jongetje heeft met Sint Maarten in totaal 126 snoepjes opgehaald. In de volgende dagen eet hij er daarvan elke dag 7 op. De kolom van de variabele "aantel snoepjes dat over is" begint dus met 126, en elke stap wordt er 7 van afgetrokken. Zo'n kolom noemen we voortaan een RIJ van TERMEN: 126, 119, 112, 105, ..... De recursieve formule is dan:         volgende = vorige - 7; beginwaarde = 126. Er worden verschillende notaties gebruikt om dit in de wiskunde te noteren. De belangrijkste is die van de GRM, want daarmee gaan we het laten berekenen: an+1 = an - 7 ; a1 = 126. n is het symbool voor het nummer van de stap. Je komt ook wel tegen in examens:            F(n+1) = F(n) - 7 ; F(1) = 126. n is hier net zo'n symbool als de x; hier heb je alleen functiewaarden voor gehele waarden van x.

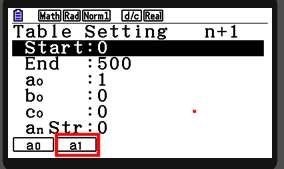
Zet de GRM in recursie-mode met MENU-8. Kies TYPE en kies daaruit de regel waarin je "Volgende = Vorige .... " herkent. Dat is de middelste regel. Om de formule in te kunnen tikken moet je de beschikking hebben over symbolen voor n en an+1 en an. Dat doe je hiermee:     en je krijgt dan te zien:   . Je kunt dan de recursieve formule intikken, gevolgde door EXE. Niet meteen naar TABLE gaan. Eerst nog het begingetal invoeren m.b.v. SET. Als je met a1 wilt beginnen, kies dan a1 i.p.v. a0, zet die op 126 en zet START op 1. Is dat gelukt, gebruik dan EXE om te bevestigen. Daarna kun je TABLE kiezen. Met de pijltjes-knop kun je naar beneden scrollen, en zien wat er gebeurt. De meest rechtse kolom gebruiken we nu niet, dat doen we wel als we de optelsom van al die termen interessant vinden. Er zijn examenopgaven die dat van je vragen. Als je die rechterkolom niet ziet moet je eenmalig met SETUP (boven MENU) dat DISPAY op "on" zetten. Je ziet dat op de 18e dag de snoepjes op zijn. Je ziet dat dit een discrete vorm is van de continue lineaire functie met a = -7 en b = 126.