Opgaven. Hieronder vind je een aantal oefen-opgaven. Sommige daarvan komen uit eindexamenopgaven. Aangepast materiaal afkomstig van de website van de heer Hofstede; opgaven 1-5. 1. a. Wat is de directe formule die hoort bij de recursieve formule     an+1 = an + 3; a0 = 5 ? b. Wat is de directe formule die hoort bij de recursieve formule     an+1 = an × 3; a0 = 5 ? c. Wat is de recursieve formule die hoort bij de directe formule     an = 5 × 0,9n ? d. Wat is de recursieve formule die hoort bij de directe formule     an = 5 × n - 7 ? 2. Geef van de volgende rijen een directe vergelijking en een recursievergelijking a. 12 ... 26 ... 40 ... 54 ... 68 .... b. 40 ... 60 ... 90 ... 135 .... 3. Voor een rij getallen geldt dat u4 = 162 en u7 = 4374. a. Bereken u9 als het een rekenkundige rij is b. Bereken u9 als het een meetkundige rij is. 4. Een octaaf op een piano bestaat uit 12 tonen.     Luister De frequenties van deze tonen vormen een meetkundige rij. De centrale C van een piano heeft frequentie 256 Hz. De C die twaalf tonen hoger ligt heeft frequentie 512 Hz, dus 2 maal zo hoog. Dat betekent dat elk van de 12 stapjes naar een volgende (witte of zwarte) toets een 12√2 keer zo hoge frequentie heeft als zijn voorganger. Want (12√2)12 = 2. Dit kwamen we bij berekeningen van de groeifactor bij exponentiële functies in de vierde klas al tegen. 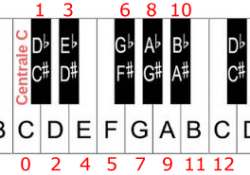a. Stel een recursieve formule op voor de frequentie fn van toon nummer n als de C nummer 0 heeft. b. Wat zijn de frequenties van de tonen D E F G A B die op de centrale C volgen? Rond af op gehele getallen. 5. Papierformaten zijn niet zomaar gekozen.... Als je een kopietje op A4-papier wilt vergroten naar A3-formaat, dan moet dat A3-papier natuurlijk wel dezelfde verhoudingen hebben als het A4 papier, anders zou de "vorm" van je plaatje veranderen. Verder zijn de papierformaten zó gekozen dat de lengte van een volgend kleiner formaat steeds gelijk is aan de breedte van de vorige. Want dan vormen twee velletjes A-5 naast elkaar precies één vel A4 (een dubbel te vouwen boekje). Hiernaast zie je hoe een vel A0-papier is onderverdeeld in steeds kleinere formaten. Er is afgesproken dat A0 een oppervlakte van 1 m2 heeft. Nu moet de verhouding bij A0 gelijk zijn aan de verhouding bij A1. Dus 2B:L = L:B. Dus 2B2 = L2. Dus L = B×√2. 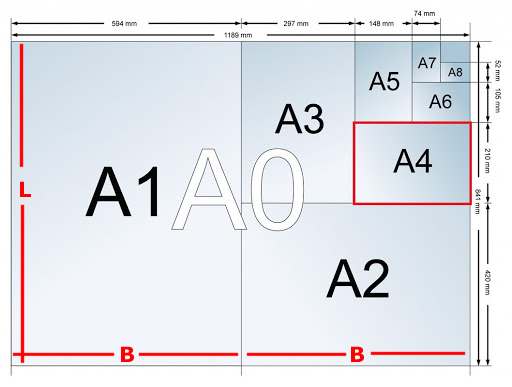Dan heeft A0 de volgende afmetingen: 119 × 84 cm. (Product = 9996 cm2; Verhouding = 1,417 : 1) We krijgen daarom een meetkundige rij die begint bij A0 = 119 cm en die telkens √2 keer kleiner wordt, d.w.z. vermenigvuldigd wordt met 0,707. a. Stel een recursieve formule op voor de lengte van de papieren uit de rij A0, A1, A2, ...... b. Wat zijn de lengte en breedte van A4? Controleer je antwoord door een A4-vel op te meten. Ook de oppervlaktes van de opeenvolgende papiersoorten vormen een meetkundige rij. Daarvoor geldt natuurlijk de recursieve formule   On+1 = 0,5 × On   met O0 = 1000000 mm2 c. Onderzoek met deze formule welk papiernummer voor het eerst een oppervlakte kleiner dan 1 mm2 heeft. 6. Disk a. Bereken het totale aantal abonnees na 6 maanden. (Totaal aantal = 90 + optelsom lineaire rij die begint met a1 = 17) b. Na hoeveel maanden is het aantal abonnees voor het eerst boven de 1000 uitgekomen? 7. Muziek op CD's 8. WK 2010 9. Wereldbevolking 10. Aardbevingen In de provincie Groningen vinden, als gevolg van gasproductie, regelmatig aardbevingen plaats. In 2013 is daar grootschalig onderzoek naar gedaan. Er werd er gekeken naar het verband tussen de gasproductie en aardbevingen. Zo zijn er bijvoorbeeld in 1993 zeven aardbevingen geweest en is er 42 miljard kubieke meter gas is geproduceerd. De magnitude, de kracht van een aardbeving, wordt uitgedrukt in een getal op de schaal van Richter. Het totaal aantal voelbare aardbevingen (met magnitudes hoger dan 1,5) tussen april 1994 (n = 0) en maand   n   is te beschrijven als een meetkundige rij   An. Uit de meting volgde dat   A0 = 12   en   A220 = 200. a. Stel de recursieve formule voor   An   op b. Voorspel het aantal aardbevingen (> 1,5 magn.) in januari 2000. 11. Cupcakes