Recursieve formules

Een recursief model beschrijft een proces waarbij de onafhankelijk variabele in (kleine) stapjes verloopt.
In veel gevallen is dat de tijd. De afhankelijk variabele wordt dan een rij van termen.

Zo'n model bestaat uit een beginwaarde en een regel die aangeeft hoe je telkens de volgende-waarde uit de vorige-waarde kunt berekenen.

Voorbeelden:

De rij van Fibonacci. Beginwaarden zijn F(1) = 1 en F(2) = 1.
De regel in woorden: "Tel de waarden van de vorige en de voor-vorige termen bij elkaar op".
De regel in formule-vorm: F(n+2) = F(n-1) + F(n) voor elk natuurlijk getal n > 0.

De rij ziet er dan als volgt uit: 1 , 1 , 2 , 3 , 5 , 8 , 13 , ...... Dit zijn de termen van de rij.

De lineaire rij. Beginwaarde is gegeven ; notatie: u(0) of u₀.
De regel in woorden: "Tel er een vast getal bij op".
De regel in formule-vorm: u(n+1) = u(n) + v voor elk natuurlijk getal n.
De waarde van v is dus het vaste verschil tussen twee opeenvolgende termen van de rij.

De rij ziet er bijvoorbeeld als volgt uit: 1 , -2 , -5 , -8 , ......
Het vaste verschil is hier -3.

De exponentiële rij. Beginwaarde is gegeven ; notatie: u(0) of u₀.
De regel in woorden: "Vermenigvuldig met een vast getal".
De regel in formule-vorm: u(n+1) = u(n)·r voor elk natuurlijk getal n.
De waarde van r is dus de vaste verhouding tussen twee opeenvolgende termen van de rij.
De letter r komt van het woord "ratio" en heet in NL "de reden".

De rij ziet er bijvoorbeeld als volgt uit: 2 , 6 , 18 , 54 , 162, ......
De vaste reden is hier 3.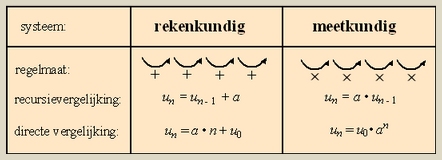

De grenswaarde (áls die bestaat): wat gebeurt er met de term als n → ∞?
Je kunt een grenswaarde, als die er is, het best met de botte-bijl-methode van de GRM vinden.
De recursieve formule is bijvoorbeeld: u(n+1) = 1,5·u(n) - (u(n))² ; u(0) = 0,7.

Je maakt een tabel met beginwaarde 0,7 en laat de waarde van n lekker groot worden.

Als er een grenswaarde is, dan moet voor die waarde gelden dat de volgende even groot blijft als de vorige!
In formule: u(n+1) moet gelijk zijn aan u(n), en wel gelijk aan de grenswaarde L (L van limiet).
En die voorwaarde levert een vergelijking op die we kunnen oplossen.

Een voorbeeld zal het duidelijk maken.
De recursieve formule is bijvoorbeeld weer: u(n+1) = 1,5·u(n) - (u(n))² ; u(0) = 0,7.
In de limiet (grens) moet dus gelden: L = 1,5L - L².
Los deze vergelijking op en je vindt de waarde van L. Dat kan met de GRM en intersect, maar deze kwadratische vergelijking is wel te doen met ontbinden in factoren.
Balansmethode: L² - 0,5L = 0 ; L·(L-0,5) = 0 ; dus L=0 of (L-0,5)=0 ; dus L = 0,5
(N.B.: De limietwaarde L=0 lukt alleen als je een beginwaarde 1,5 neemt! Dan is de volgende term meteen nul.)

Examenopgaven om te proberen:
2018-I    Toren van achtvlakken 19, 20, 21
2012-I    Halvering van vlakken 16, 17
2018-II   Cupcakes 8,9
2017-II   Gitaar 15, 16, 17
2013-II   WK 2010 9, 10
2019-I    Groningse aardbevingen 9

Extra bijzondere opgaven om te proberen:

Verschil-rijen