Theorie over Lineaire en Exponentiële rijen.
Bevat voor een deel aangepast materiaal afkomstig van de website van de heer Hofstede

RECURSIEVE FORMULES voor lineaire en exponentiële rijen

Hieronder staan een paar "verhaaltjes" waar een rij getallen bij hoort.
Schrijf van elke rij een recursieformule op.

a. Ik heb een bedrag van €400,- op een bankrekening staan en krijg daarover elk jaar 4% rente.

b. Je reactievermogen wordt slechter als je meer glazen alcohol hebt gedronken.
In het verkeer is de reactietijd van een proefpersoon gelijk aan 0,8 seconden.
Bij elk gedronken glas alcohol wordt die tijd 0,2 seconden langer.

c. De eerste keer dat men een oproep om geld te doneren aan een goed doel uitzendt, levert dat
58000 donaties op. Elke volgende keer wordt dat aantal donaties kleiner, omdat het aantal nieuwe
mensen dat bereikt wordt kleiner wordt. Het blijkt dat het aantal donaties bij elke volgende
uitzending steeds ongeveer 10% kleiner wordt.

d. Bij een sponsorloop krijgt Ans van haar buurvrouw €4,- en verder voor elk rondje nog eens
€0,15 extra.

Heb je intussen door dat hier twee verschillende systemen aan 't werk zijn?
a en c horen bij elkaar, en b en d ook......

Dat komt hierdoor:
Bij b en d ziet de recursievergelijking eruit als u_n+1 = u_n + a (waarbij a eventueel een negatief getal is).
De regelmaat van deze rijen is, dat de opeenvolgende termen steeds PLUS hetzelfde getal zijn.
Zo'n rij is dus een Lineaire rij. Hij wordt in deze contekst ook wel Rekenkundige rij genoemd.

Bij a en c ziet de recursievergelijking er uit als u_n+1 = u_n × a
De regelmaat van deze rijen is, dat de opeenvolgende termen steeds KEER hetzelfde getal zijn.
Zo'n rij is dus een Exponentiële rij. Hij wordt in deze contekst ook wel Meetkundige rij genoemd.

Dus:

Zie je dat in het plaatje hierboven niet staat: u_n+1 = u_n + a , maar u_n = u_n-1 + a ?
En begrijp je dat dat gewoon dezelfde recursieve formules zijn? Volgende = Vorige + a.

DIRECTE FORMULES voor lineaire en exponentiële rijen

Omdat een meetkundige en een rekenkundige rij in feite hetzelfde zijn als een lineair en een exponentiele functie kunnen we voor dit soort rijen ook de "gewone" formule van vroeger gebruiken. Daarbij is de x nu vervangen door een n en de y door een u_n.
Zo'n "gewone" formule heet bij rijen een directe formule. Het woord zegt het eigenlijk al: je kunt een u_n direct uitrekenen als je n weet, zonder alle vorige u_n te moeten berekenen.
Maar er is een belangrijk verschil: Rijen zijn discreet.
De n-waarden kunnen alleen gehele getallen zijn. 't Zijn immers de nummers!
Dat betekent ook dat een eventuele grafiek er niet uit zal zien als een kromme, maar als een verzameling losse stippen.

SAMENGEVAT:

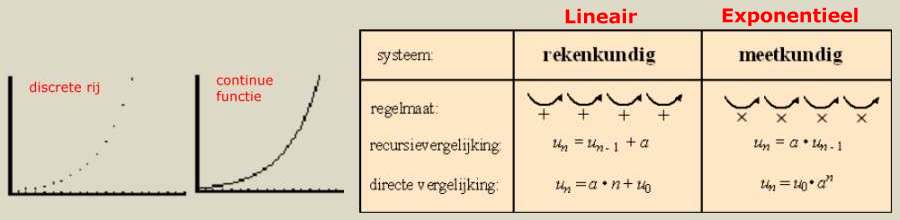N.B.: Bij een directe formule zet je altijd u_n = ..., en nooit u_n+1 = ...

NOG een SAMENVATTING over het wisselen tussen recursieve en directe formules:

Opmerking over de notatie bij lineaire en exponentiële rijen.

Bij lineaire rijen wordt dikwijls in plaats van de letter a de letter v gebruikt;
v is het verschil tussen twee opeenvolgende termen.

Bij exponentiële rijen wordt dikwijls in plaats van de letter a de letter r gebruikt;
r is de ratio (= verhouding) tussen twee opeenvolgende termen.

De grenswaarde (áls die bestaat): wat gebeurt er met de term als n → ∞?
Je kunt een grenswaarde, als die er is, het best met de botte-bijl-methode van de GRM vinden.
De recursieve formule is bijvoorbeeld: u(n+1) = 1,5·u(n) - (u(n))² ; u(0) = 0,7.

Je maakt een tabel met beginwaarde 0,7 en laat de waarde van n lekker groot worden.